算法笔记

1
Algorithm(算法)和Program(程序)的区别
| Algorithm | Programe |
|---|---|
| Design(设计过程) | Implementation(执行过程) |
| Domain knowledge(对应领域知识) | programmer(程序员) |
| All language(所有语言皆可) | programe language(仅程序语言:C、C++、Java、Python) |
| No Hardware/software and OS | H/W and OS |
| Analyse(分析) | Testing(调试) |
1.2
Characteristics of Algoithm (算法特性)
- Input 0个或更多
- output 至少一个
- Definiteness (确定性) 明确
- Finiteness (有限性)不能是无限的,要有结束
- effectiveness(效力)
1.3
How to Analyse an Algorithm
criteria(准则):
time :一个操作占用一个单元时间似乎太过于细节,所以选择一个语句作为一个单元时间,用O(1)表示,代表常数1
space:用S(n)表示,有几个变量,写S(n)=几word,为啥用word,因为我们不知道变量的类型,或者说变量的类型不唯一
data transferred(已传输的数据) network consumption
power consuming
CPU Registers (CPU寄存器)
1.4
Frequency Count Method

f(n)=2n+3 ==> O(n)
for语句是n+1,i<n需要判断n+1次
fn应是整个流程要进行的最小单元语句的次数

S(n)=n+3 ==> O(n)
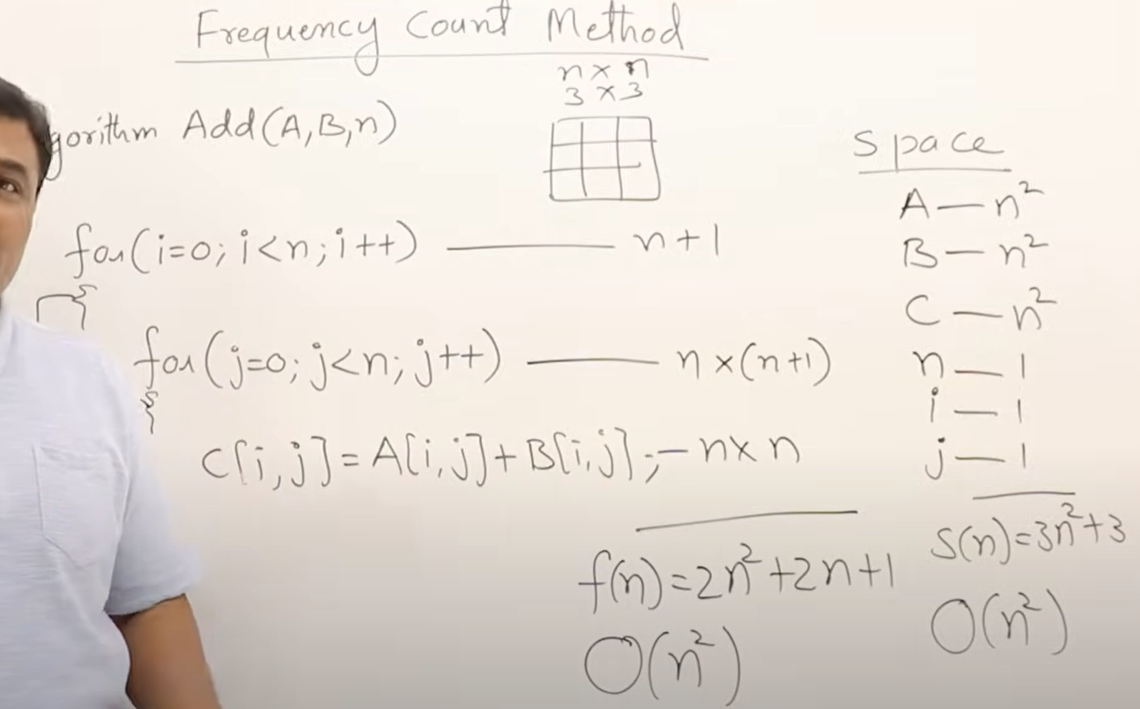

1.5
Time Complexity
下面是一些例子

时间复杂度用一条执行语句算

这个比较难算,我觉得我是算不出的
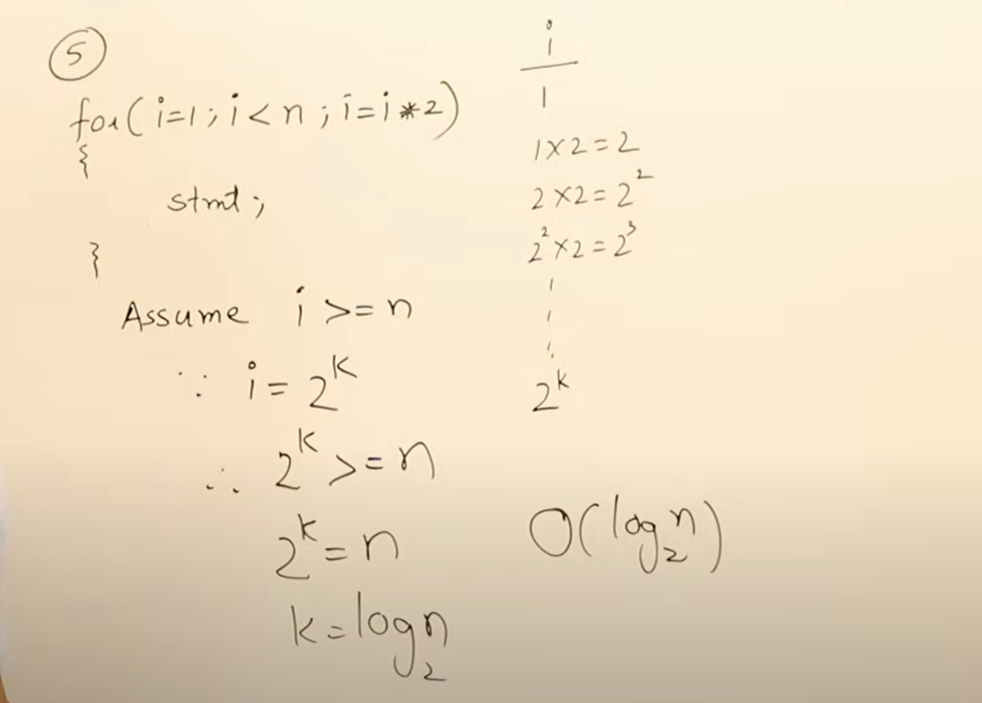

这段语句不是嵌套的,所以复杂度不是n方是n
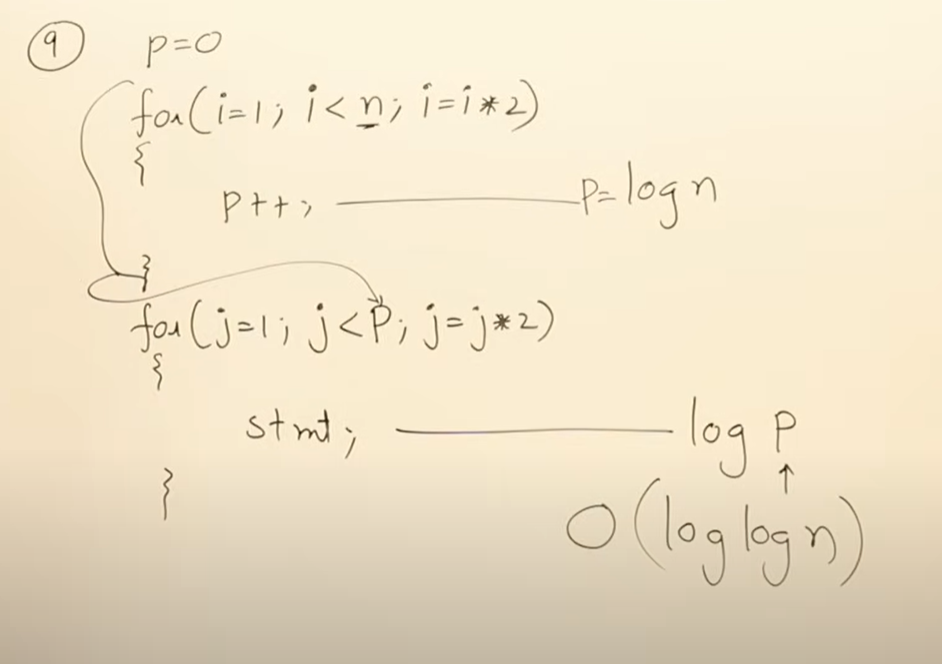
注意这个是O(loglogn)

第一句可以写n也可以写n+1,这没有什么区别,记一些常用的对于计算有帮助


一个算法有最好情况和最坏情况,比如上面这个,最好情况就是m和n相同O(1),最坏的情况是两者不同,并且需要很多次O(n)。

同样,这个也是分情况的

将上算法做部分修改删掉了n<5的情况,算法就没有最好和最坏情况了,这里想说的应该是复杂度和判断语句有关
1.7

时间复杂度快慢比较

大O ——上界
欧米噶Ω ——下界
西塔θ —— 平均界
大O的定义解释
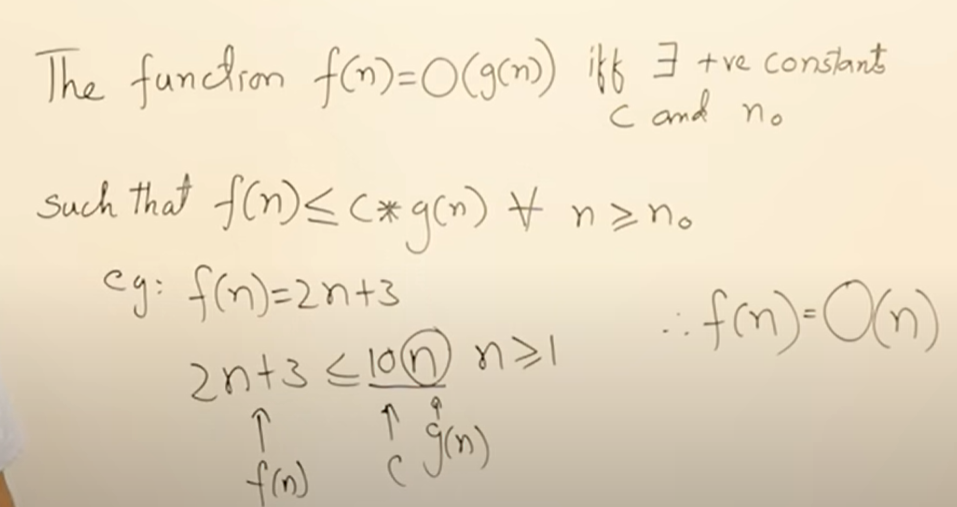
f(n)<=__ 横线填一个带n的式子,要比左侧大,图中写的是10n,根据这个式子可以得出对n的一个条件n>1
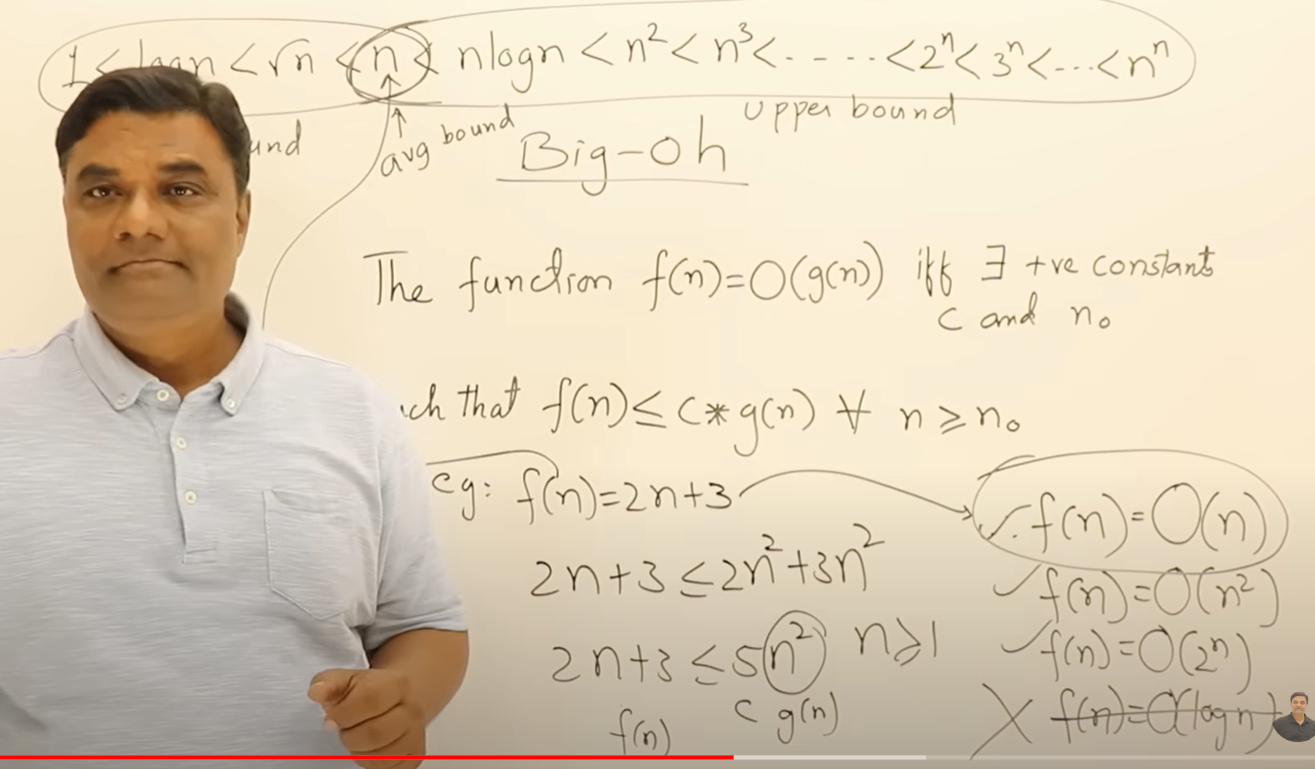
以n为界限,包括n和他之后的都是upper bound,包括他之前的都是lower bound ,n是average bound
fn=On,fn=On方,fn=O2的n次方都对,但是我们总是写最小的那个,那是useful的
fn=Ologn不对
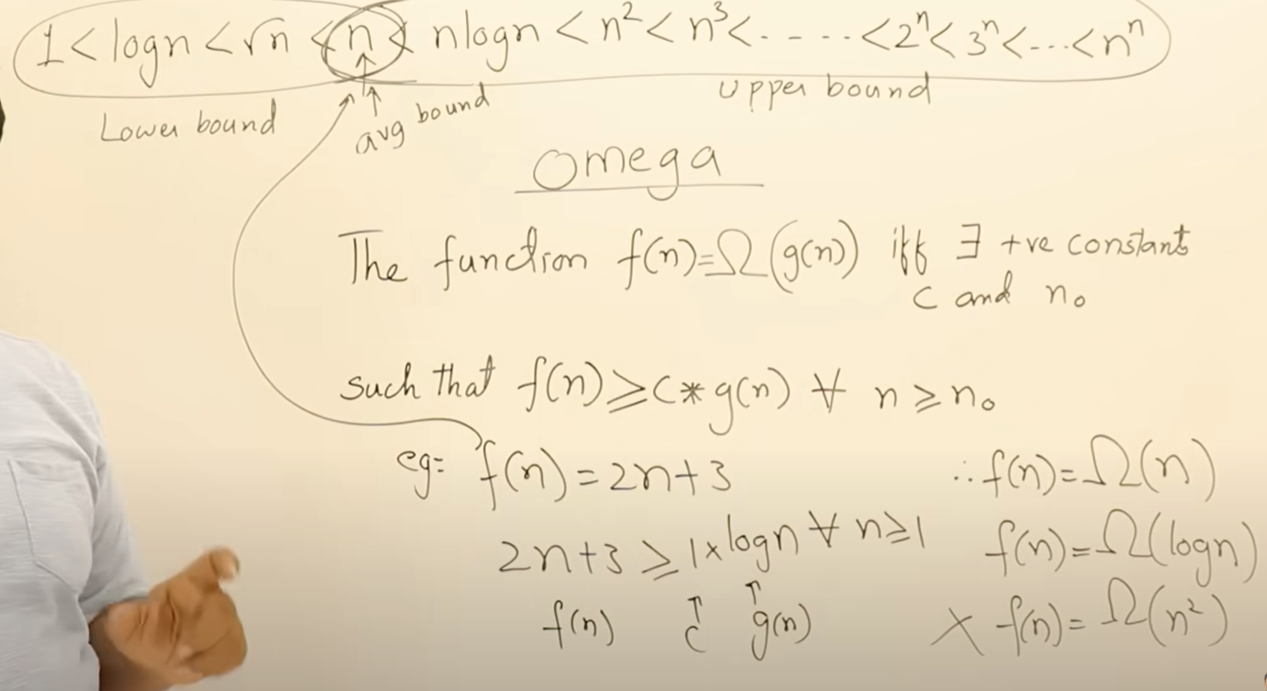
Ω的定义,和大O定义相反
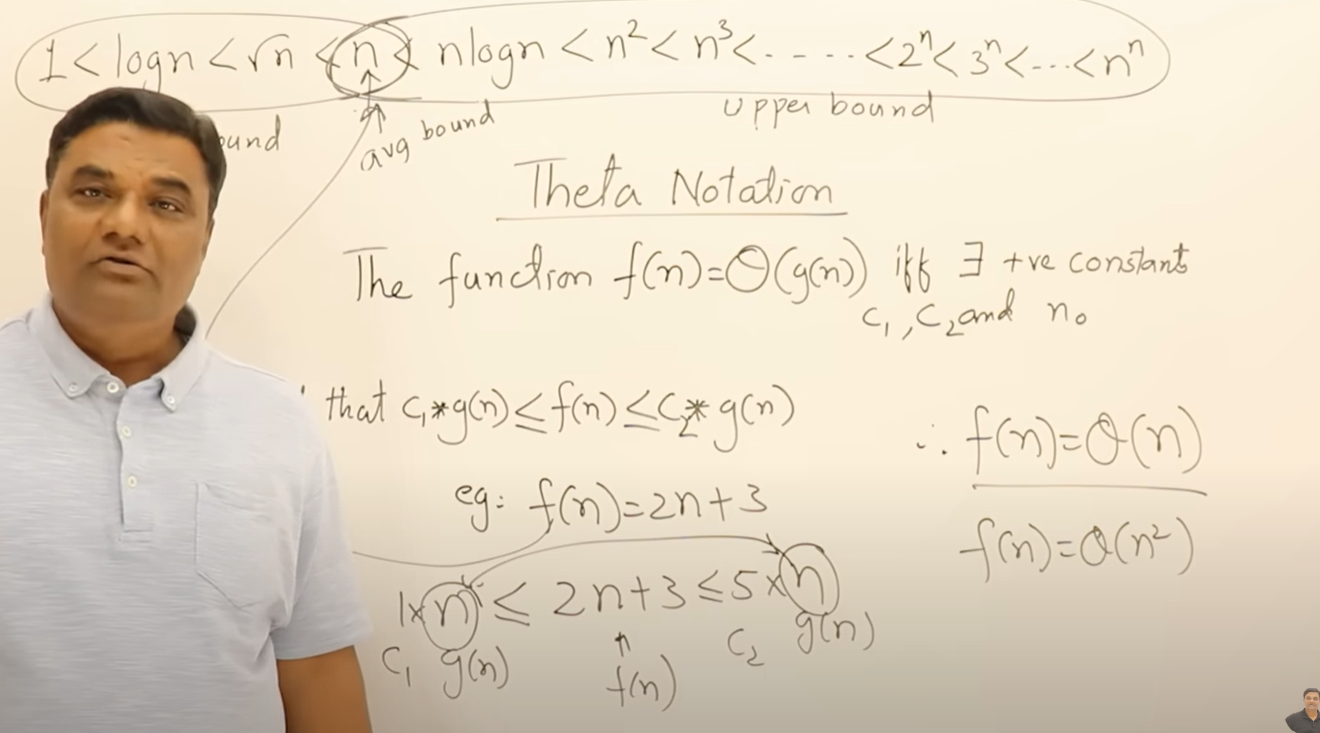
θ的定义类似是两者的定义的结合,这时fn=希尔他n不能写其他
这些都可以用来表示算法的复杂度,这和算法的最好情况和最坏情况无关,不要混淆
下面是一些例子
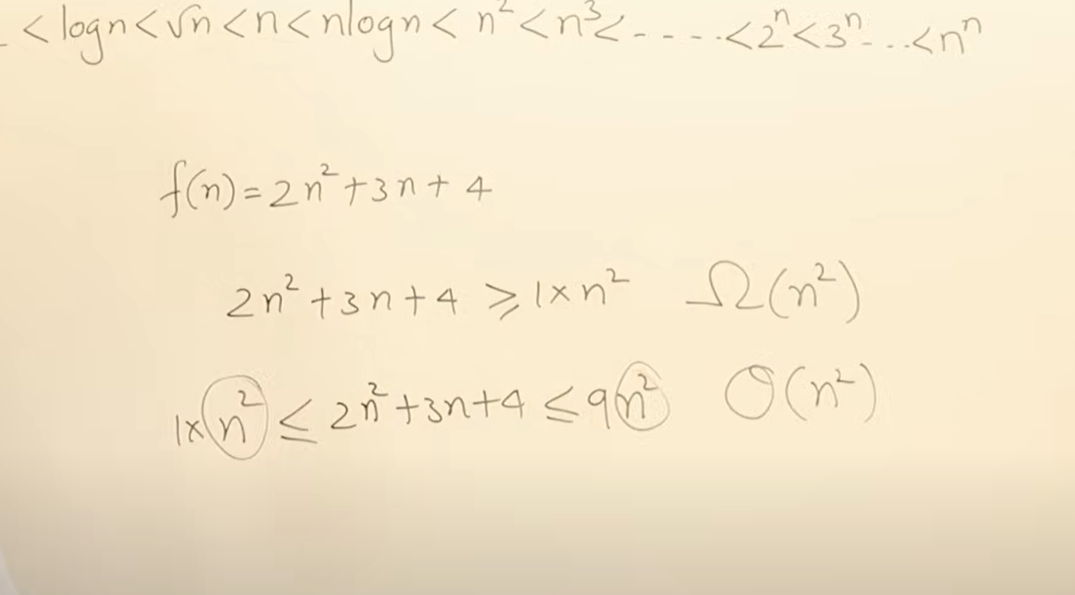
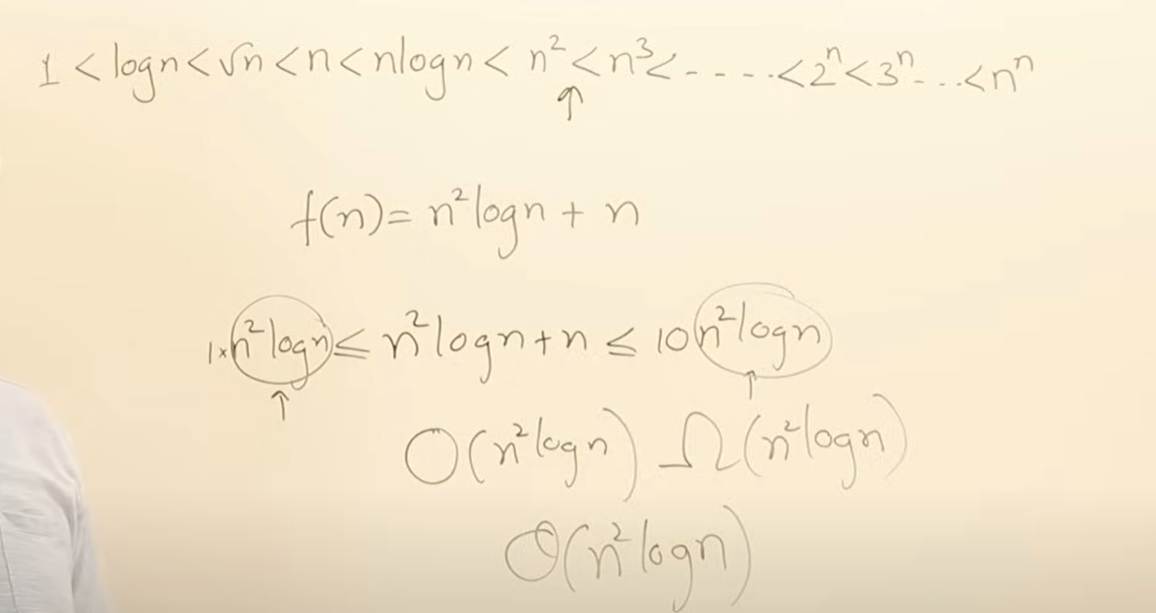
介于n方和n三次方
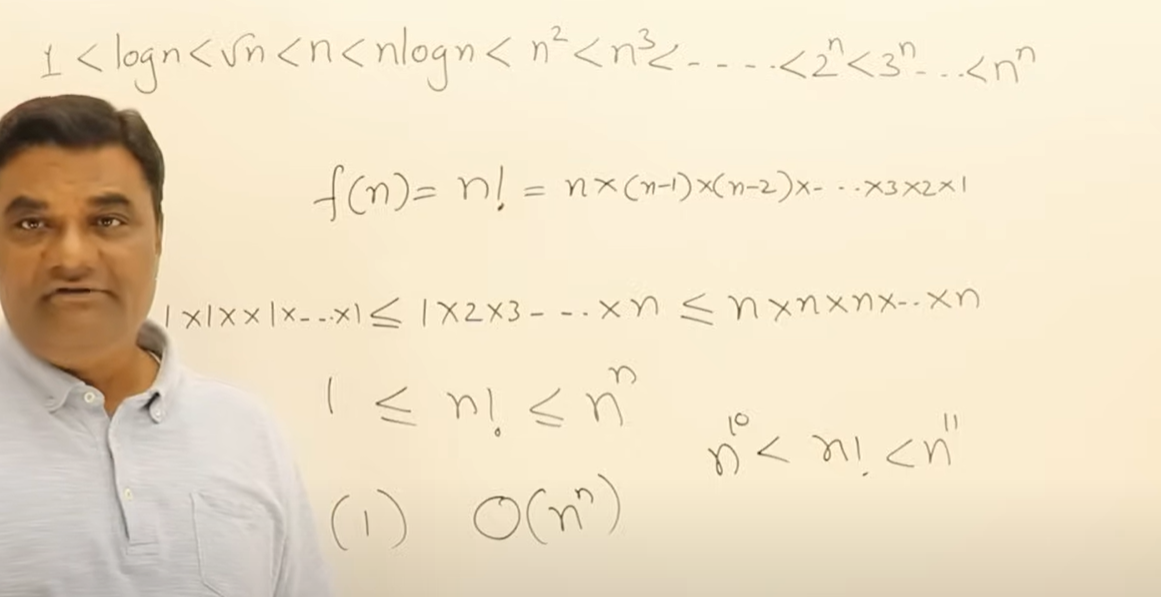
n的阶乘写不出希尔他的形式,只能写出Ω(1)和O(n的n次方)
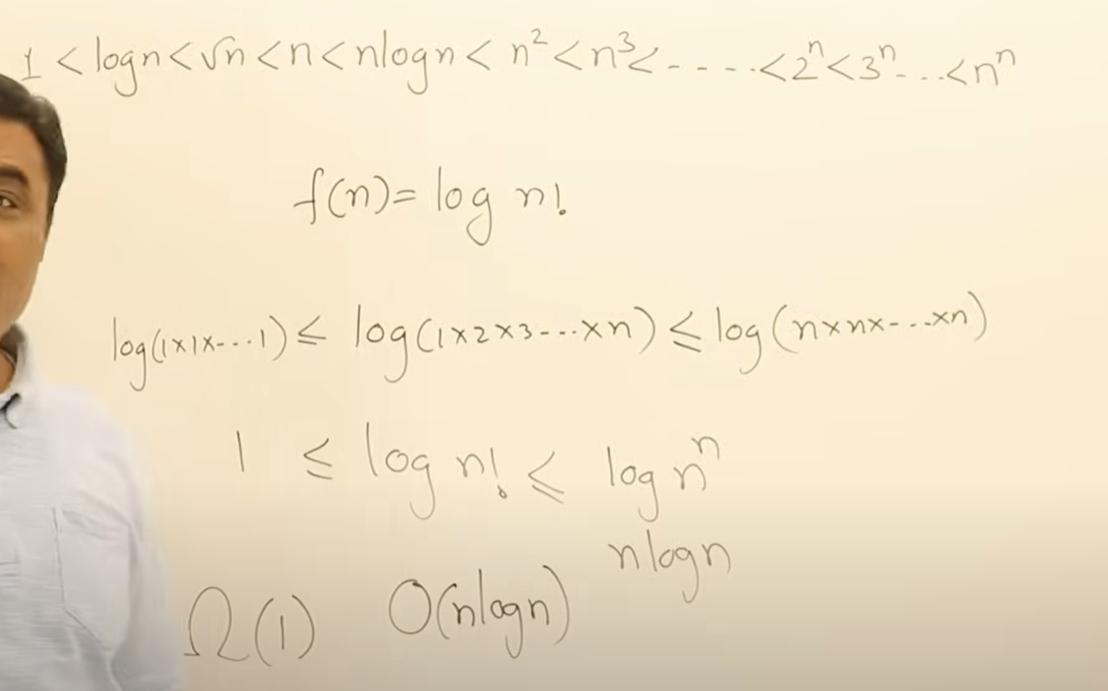
1.9
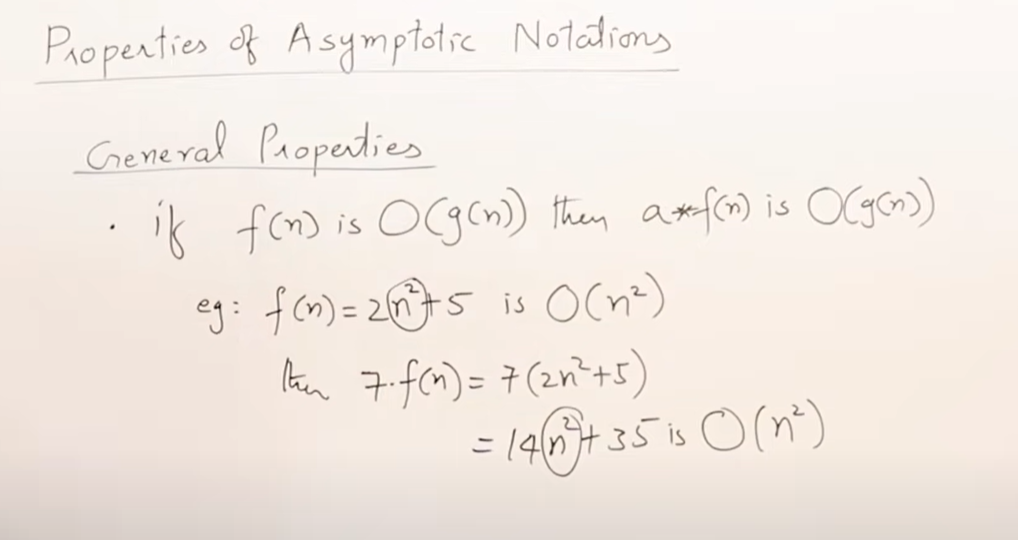
扩大常数倍大O不变
Ω和θ也一样
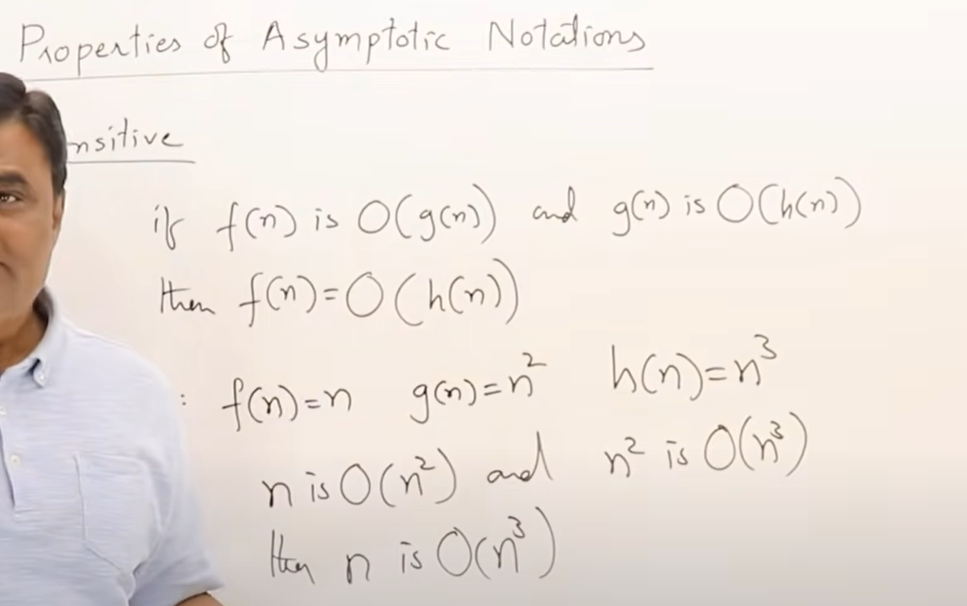
大O有传递性
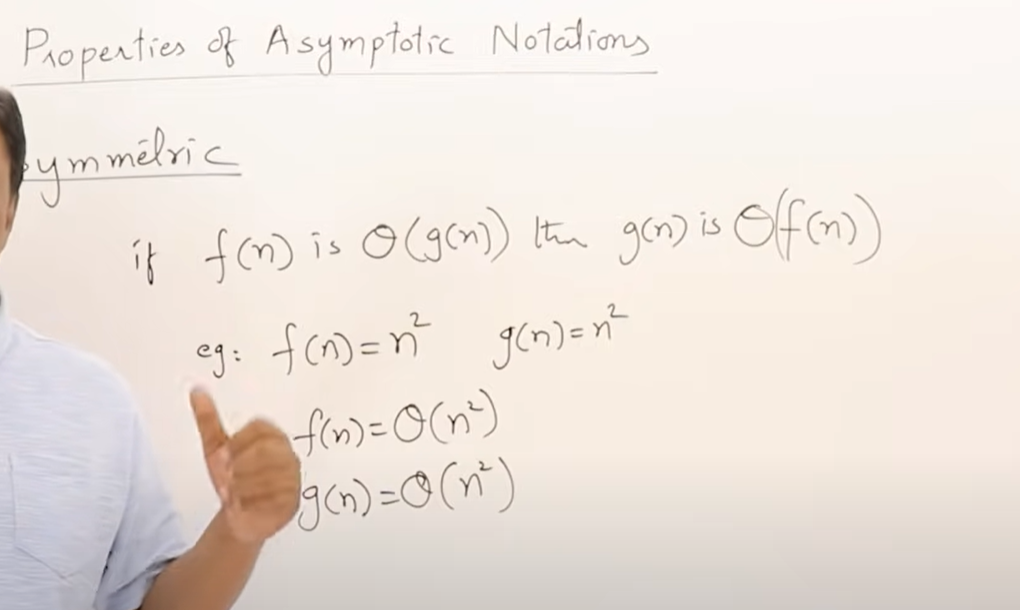
θ具有对称性

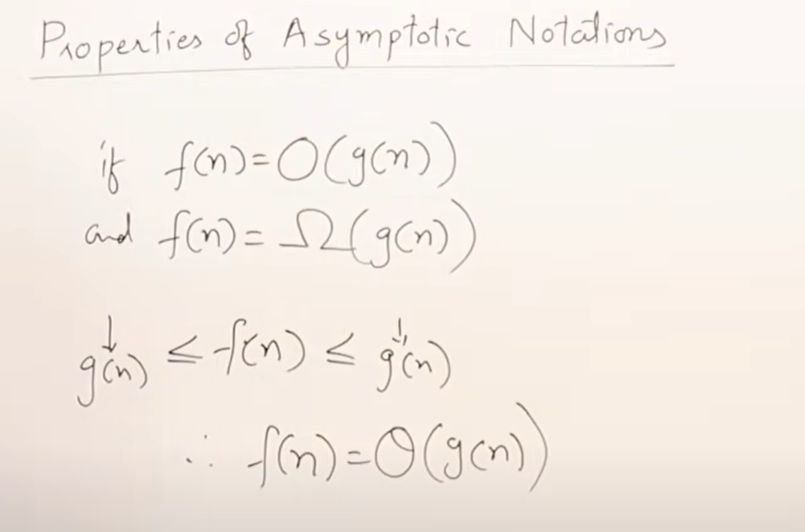
f(n)=O(g(n))andf(n)=Ω(g(n))==》f(n)=θ(g(n))
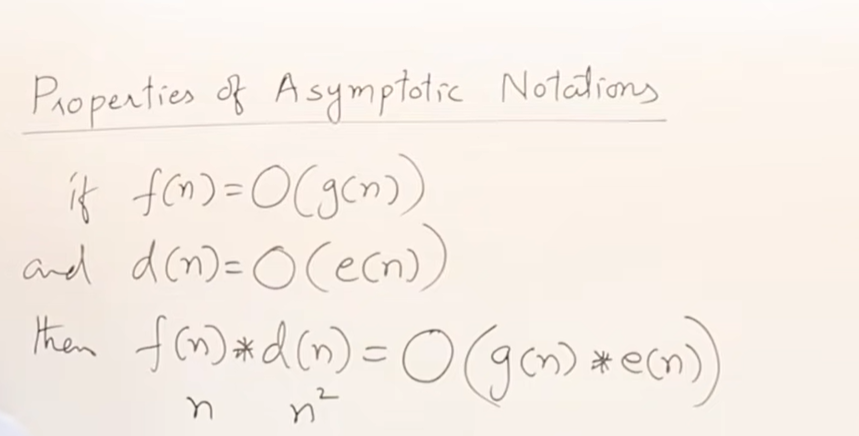
两个function相乘,O也是相乘

比较两个function的O时,可以同时加log
最后loglogn特别小,所以比较logn的数量即可

第四条我没推出来,查是两次换底公式,没搞明白

可以多次log约

这两个function是同级的

这两个不是同级的

不是分段的,g2>g1
1.11

可以用任何符号(O、Ω、θ)表示function,这和最好最坏情况没有关系

二分查找树的高度是logn,n是树上的元素个数,最坏的情况是查找位于叶子的元素,也就是需要查找树的高度次,也就是logn,所以最坏的情况下查找效率是logn

但是,也有树是倾斜的情况,也是二叉查找树,但是此时的最坏情况的查找效率就是n了
所以最坏的情况的效率取决于树的高度
1.12
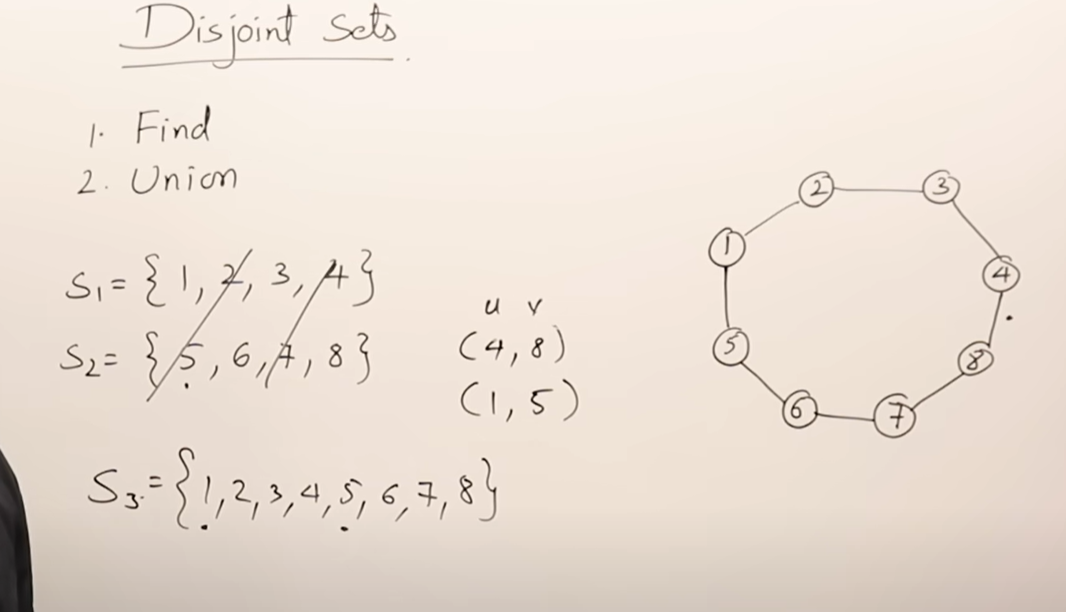
两个不相连的set,通过查找和联合,使其成为一个圆,知道在图中有一个圆。
借助这个用于图转生成树,确保树中没有循环
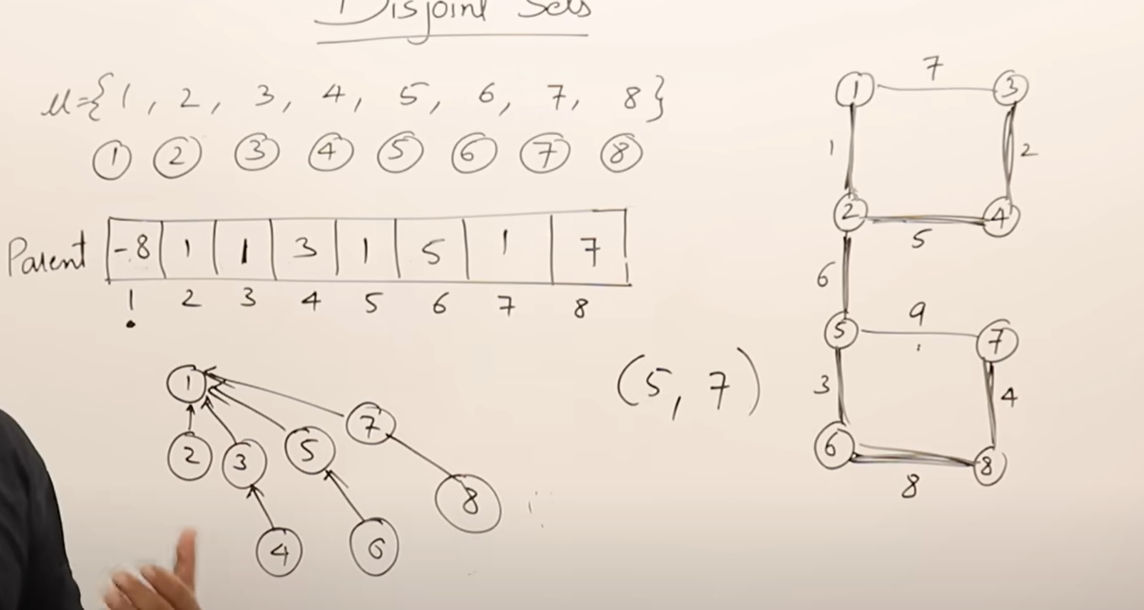
选择图中合适的边用于生成树
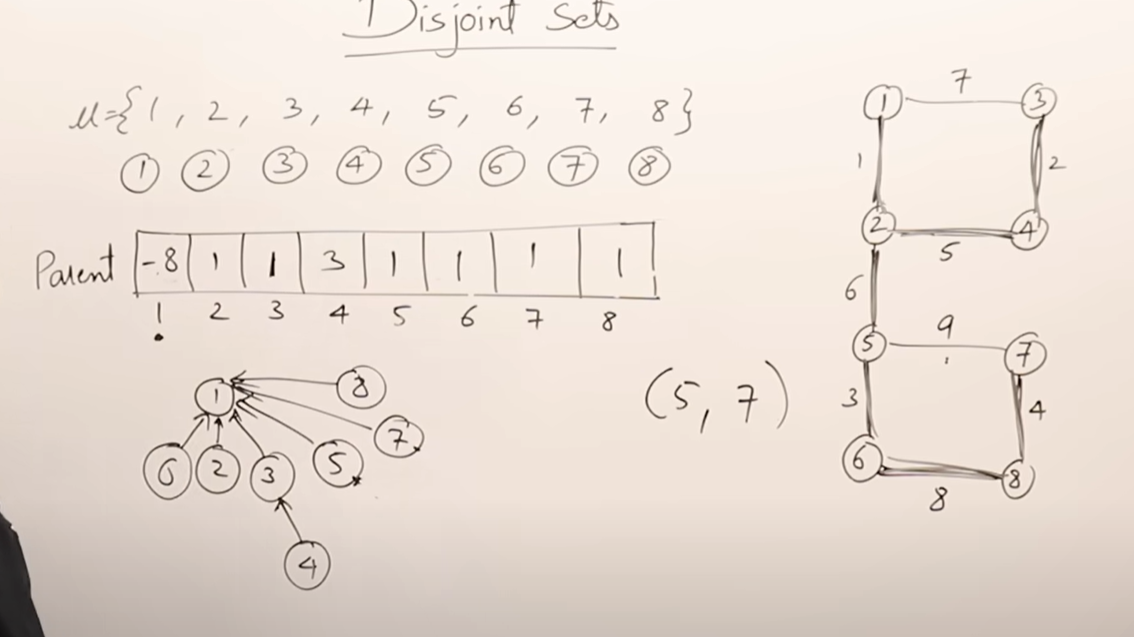
当发现一个节点的最终父节点时,可以在数组中将其父节点改为最终父节点,方便下次查找,我们叫这种查找叫折叠查找,不太懂。
2
Divide and Conquer(分治法)